Time series analysis ARIMA | SARIMA

 

What is Time Series?

• According to the wikipedia, A time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. For example, stock prices over a fixed period of time, hotel bookings, ecommerce sales, waether cycle reports etc.

• Time series analysis comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series forecasting is the use of a model to predict future values based on previously observed values.

Examples of time series data:

• Stock prices, Sales demand, website traffic, daily temperatures, quarterly sales.

Components of a Time Series:

• Trend
• Seasonality

What is a TREND in time series?

• Trend is a pattern in data that shows the movement of a series to relatively higher or lower values over a long period of time.

• Trend usually happens for some time and then disappears, it does not repeat. For example, some new kaggle kernels, it goes trending for a while, and then disappears. There is fairly any chance that it would be trending again.

A trend could be :

• UPTREND: Time Series Analysis shows a general pattern that is upward then it is Uptrend.
• DOWNTREND: Time Series Analysis shows a pattern that is downward then it is Downtrend.
• HORIZONTAL TREND: If no pattern observed then it is called a Horizontal or stationary trend.

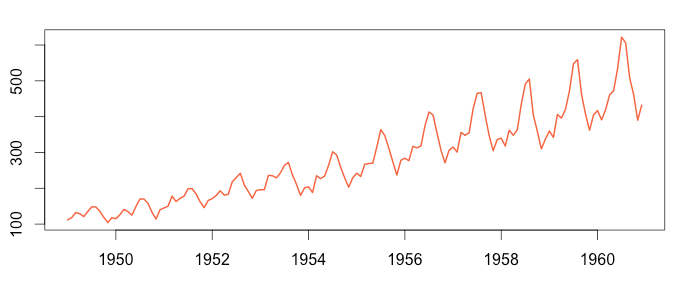
What is SEASONALITY?

• Predictable pattern that recurs or repeats over regular intervals. Seasonality is often observed within a year or less.

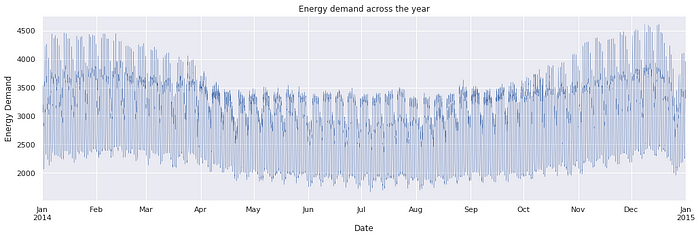
Modelling and evaluation Techniques:

• MODELS: Naive approach, Moving average, Simple exponential smoothing, Holt.s linear trend model, Auto Regression Integrated Moving Average(ARIMA), SARIMAX, etc.

• Mean Square Error(MSE), Root Mean Squared Error(RMSE)

---

AUTO-CORRELATION:

• Before we decide which model to use, we need to look at auto-correlations

• Autocorrelation is the most important concept in time series. It is precisely what makes modeling them so difficult.

• Autocorrelation is the measure of the degree of similarity between a given time series and the lagged version of that time series over successive time periods. It is similar to calculating the correlation between two different variables except in Autocorrelation we calculate the correlation between two different versions Xt and Xt-k of the same time series

• In time series, the current value depends on past values. If the temperature today is 80 F, tomorrow it is more likely for the temperature to be around 80 F rather than 40 F.

• If you swap the first and tenth observations in tabular data, the data has not changed one bit. If you swap the first and tenth observations in a time series, you get a different time series. Order matters. Not accounting for autocorrelation is almost as silly as this timeless classic.

PARTIAL AUTO-CORRELATION:

• Another useful method to examine serial dependencies is to examine the partial autocorrelation function (PACF) – an extension of autocorrelation, where the dependence on the intermediate elements (those within the lag) is removed.

Once we determine the nature of the auto-correlations we use the following rules of thumb.

• Rule 1: If the ACF shows exponential decay, the PACF has a spike at lag 1, and no correlation for other lags, then use one autoregressive (p)parameter

• Rule 2: If the ACF shows a sine-wave shape pattern or a set of exponential decays, the PACF has spikes at lags 1 and 2, and no correlation for other lags, the use two autoregressive (p) parameters

• Rule 3: If the ACF has a spike at lag 1, no correlation for other lags, and the PACF damps out exponentially, then use one moving average (q) parameter.

• Rule 4: If the ACF has spikes at lags 1 and 2, no correlation for other lags, and the PACF has a sine-wave shape pattern or a set of exponential decays, then use two moving average (q) parameter.

• Rule 5: If the ACF shows exponential decay starting at lag 1, and the PACF shows exponential decay starting at lag 1, then use one autoregressive (p) and one moving average (q) parameter.

Removing serial dependency.

Serial dependency for a particular lag can be removed by differencing the series. There are two major reasons for such transformations.

• First, we can identify the hidden nature of seasonal dependencies in the series. Autocorrelations for consecutive lags are interdependent, so removing some of the autocorrelations will change other auto correlations, making other seasonalities more apparent.

• Second, removing serial dependencies will make the series stationary, which is necessary for ARIMA and other techniques.

DURBIN-WATSON TEST:

• Another popular test for serial correlation is the Durbin-Watson statistic.
• Durbin-Watson test is used to measure the amount of autocorrelation in residuals from the regression analysis. Durbin Watson test is used to check for the first-order autocorrelation.

Assumptions for the Durbin-Watson Test:

• The errors are normally distributed and the mean is 0.

• The errors are stationary.

• The null hypothesis and alternate hypothesis for the Durbin-Watson Test are

    H0: No first-order autocorrelation.
    H1: There is some first-order correlation.

The Durbin Watson test has values between 0 and 4. Below is the table containing values and their interpretations:

• 2: No autocorrelation. Generally, we assume 1.5 to 2.5 as no correlation.
• 0- <2: positive autocorrelation. The more close it to 0, the more signs of positive autocorrelation.
• greater 2 -4: negative autocorrelation. The more close it to 4, the more signs of negative autocorrelation.

---

TIME SERIES MODELING - ARIMA, SARIMA

ARIMA

• Autoregressive Integrated Moving Average, or ARIMA, is a forecasting method for univariate time series data.

• As its name suggests, it supports both an autoregressive and moving average elements. The integrated element refers to differencing allowing the method to support time series data with a trend.

• A problem with ARIMA is that it does not support seasonal data. That is a time series with a repeating cycle.

• ARIMA expects data that is either not seasonal or has the seasonal component removed, e.g. seasonally adjusted via methods such as seasonal differencing.

SARIMA

• Seasonal Autoregressive Integrated Moving Average, SARIMA or Seasonal ARIMA, is an extension of ARIMA that explicitly supports univariate time series data with a seasonal component.

• It adds three new hyperparameters to specify the autoregression (AR), differencing (I) and moving average (MA) for the seasonal component of the series, as well as an additional parameter for the period of the seasonality.

• A seasonal ARIMA model is formed by including additional seasonal terms in the ARIMA.

• The seasonal part of the model consists of terms that are very similar to the non-seasonal components of the model, but they involve backshifts of the seasonal period.

The general process for ARIMA models is the following:

• Visualize the Time Series Data
• Make the time series data stationary
• Plot the Correlation and AutoCorrelation Charts
• Construct the ARIMA Model or Seasonal ARIMA based on the data
• Use the model to make prediction

---

PYTHON IMPLEMENTATION

1. BASIC STEPS OF A PROJECT:

In [1]:

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
%matplotlib inline

In [2]:

df=pd.read_csv('../input/perrin-freres-monthly-champagne-sales/Perrin Freres monthly champagne sales millions.csv')

In [3]:

df.head()

Out[3]:

	Month	Perrin Freres monthly champagne sales millions ?64-?72
0	1964-01	2815.0
1	1964-02	2672.0
2	1964-03	2755.0
3	1964-04	2721.0
4	1964-05	2946.0

In [4]:

## Change the Column Names 
df.columns=["Month","Sales"]
df.head()

Out[4]:

	Month	Sales
0	1964-01	2815.0
1	1964-02	2672.0
2	1964-03	2755.0
3	1964-04	2721.0
4	1964-05	2946.0

In [5]:

df.tail()

Out[5]:

	Month	Sales
102	1972-07	4298.0
103	1972-08	1413.0
104	1972-09	5877.0
105	NaN	NaN
106	Perrin Freres monthly champagne sales millions...	NaN

Here we can see that last 2 columns have null values. So we'll remove those

In [6]:

## Drop last 2 rows
df.drop(106,axis=0,inplace=True)

In [7]:

df.drop(105,axis=0,inplace=True)

In [8]:

# Convert Month into Datetime
df['Month']=pd.to_datetime(df['Month'])

In [9]:

df.head()

Out[9]:

	Month	Sales
0	1964-01-01	2815.0
1	1964-02-01	2672.0
2	1964-03-01	2755.0
3	1964-04-01	2721.0
4	1964-05-01	2946.0

In [10]:

df.set_index('Month',inplace=True)

In [11]:

df.head()

Out[11]:

	Sales
Month
1964-01-01	2815.0
1964-02-01	2672.0
1964-03-01	2755.0
1964-04-01	2721.0
1964-05-01	2946.0

In [12]:

df.describe()

Out[12]:

	Sales
count	105.000000
mean	4761.152381
std	2553.502601
min	1413.000000
25%	3113.000000
50%	4217.000000
75%	5221.000000
max	13916.000000

---

2. VISUALIZE THE DATA:

In [13]:

df.plot()

Out[13]:

<AxesSubplot:xlabel='Month'>

• #### Testing For Stationarity : When a time series is stationary, it can be easier to model.
• #### "adfuller" is a function / module used to check the STATIONARITY in dataset.

In [14]:

from statsmodels.tsa.stattools import adfuller

In [15]:

test_result=adfuller(df['Sales'])

In [16]:

#HYPOTHESIS TEST:
#Ho: It is non stationary
#H1: It is stationary

def adfuller_test(sales):
    
    result=adfuller(sales)
    
    labels = ['ADF Test Statistic','p-value','#Lags Used','Number of Observations Used']
    
    for value,label in zip(result,labels):
        print(label+' : '+str(value) )
    
    if result[1] <= 0.05:
        print("strong evidence against the null hypothesis(Ho), reject the null hypothesis. Data has no unit root and is stationary")
    else:
        print("weak evidence against null hypothesis, time series has a unit root, indicating it is non-stationary ")

In [17]:

adfuller_test(df['Sales'])

ADF Test Statistic : -1.8335930563276228
p-value : 0.363915771660245
#Lags Used : 11
Number of Observations Used : 93
weak evidence against null hypothesis, time series has a unit root, indicating it is non-stationary 

DIFFERENCING:

• Differencing is a popular and widely used data transform for making time series data stationary.

• Differencing can help stabilise the mean of a time series by removing changes in the level of a time series, and therefore eliminating (or reducing) trend and seasonality.

• Differencing shifts ONE/MORE row towards downwards.

In [18]:

df['Seasonal First Difference']=df['Sales']-df['Sales'].shift(12)

Here the value 12 is the number of index values per period of time you are calculating.

In [19]:

df.head(14)

Out[19]:

	Sales	Seasonal First Difference
Month
1964-01-01	2815.0	NaN
1964-02-01	2672.0	NaN
1964-03-01	2755.0	NaN
1964-04-01	2721.0	NaN
1964-05-01	2946.0	NaN
1964-06-01	3036.0	NaN
1964-07-01	2282.0	NaN
1964-08-01	2212.0	NaN
1964-09-01	2922.0	NaN
1964-10-01	4301.0	NaN
1964-11-01	5764.0	NaN
1964-12-01	7312.0	NaN
1965-01-01	2541.0	-274.0
1965-02-01	2475.0	-197.0

In [20]:

## Again test dickey fuller test
adfuller_test(df['Seasonal First Difference'].dropna())

ADF Test Statistic : -7.626619157213164
p-value : 2.060579696813685e-11
#Lags Used : 0
Number of Observations Used : 92
strong evidence against the null hypothesis(Ho), reject the null hypothesis. Data has no unit root and is stationary

In [21]:

df['Seasonal First Difference'].plot()

Out[21]:

<AxesSubplot:xlabel='Month'>

NOW OUR DATA IS STATIONARY.

---

AUTO-CORRELATION | PARTIAL AUTO-CORRELATION:

In [22]:

from statsmodels.graphics.tsaplots import plot_acf,plot_pacf

In [23]:

from pandas.plotting import autocorrelation_plot
autocorrelation_plot(df['Sales'])
plt.show()

/opt/conda/lib/python3.7/site-packages/pandas/plotting/_matplotlib/misc.py:443: MatplotlibDeprecationWarning: Calling gca() with keyword arguments was deprecated in Matplotlib 3.4. Starting two minor releases later, gca() will take no keyword arguments. The gca() function should only be used to get the current axes, or if no axes exist, create new axes with default keyword arguments. To create a new axes with non-default arguments, use plt.axes() or plt.subplot().
  ax = plt.gca(xlim=(1, n), ylim=(-1.0, 1.0))

In [24]:

import statsmodels.api as sm
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df['Seasonal First Difference'].iloc[13:],lags=40,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df['Seasonal First Difference'].iloc[13:],lags=40,ax=ax2)

Here these two graphs will help you to find the p and q values.

• Partial AutoCorrelation Graph is for the p-value.
• AutoCorrelation Graph for the q-value.

---

3. ARIMA MODEL

Let’s Break it Down:-

• AR: Autoregression. A model that uses the dependent relationship between an observation and some number of lagged observations.

• I: Integrated. The use of differencing of raw observations in order to make the time series stationary.

• MA: Moving Average. A model that uses the dependency between an observation and a residual error from a moving average model applied to lagged observations.

The parameters of the ARIMA model are defined as follows:

• p: The number of lag observations included in the model, also called the lag order.
• d: The number of times that the raw observations are differenced, also called the degree of differencing.
• q: The size of the moving average window, also called the order of moving average.

In [25]:

# For non-seasonal data
#p=1, d=1, q=0 or 1
from statsmodels.tsa.arima_model import ARIMA

In [26]:

model=ARIMA(df['Sales'],order=(1,1,1))
model_fit=model.fit()

/opt/conda/lib/python3.7/site-packages/statsmodels/tsa/arima_model.py:472: FutureWarning: 
statsmodels.tsa.arima_model.ARMA and statsmodels.tsa.arima_model.ARIMA have
been deprecated in favor of statsmodels.tsa.arima.model.ARIMA (note the .
between arima and model) and
statsmodels.tsa.SARIMAX. These will be removed after the 0.12 release.

statsmodels.tsa.arima.model.ARIMA makes use of the statespace framework and
is both well tested and maintained.

To silence this warning and continue using ARMA and ARIMA until they are
removed, use:

import warnings
warnings.filterwarnings('ignore', 'statsmodels.tsa.arima_model.ARMA',
                        FutureWarning)
warnings.filterwarnings('ignore', 'statsmodels.tsa.arima_model.ARIMA',
                        FutureWarning)

  warnings.warn(ARIMA_DEPRECATION_WARN, FutureWarning)
/opt/conda/lib/python3.7/site-packages/statsmodels/tsa/base/tsa_model.py:527: ValueWarning: No frequency information was provided, so inferred frequency MS will be used.
  % freq, ValueWarning)
/opt/conda/lib/python3.7/site-packages/statsmodels/tsa/base/tsa_model.py:527: ValueWarning: No frequency information was provided, so inferred frequency MS will be used.
  % freq, ValueWarning)
/opt/conda/lib/python3.7/site-packages/statsmodels/tsa/arima_model.py:472: FutureWarning: 
statsmodels.tsa.arima_model.ARMA and statsmodels.tsa.arima_model.ARIMA have
been deprecated in favor of statsmodels.tsa.arima.model.ARIMA (note the .
between arima and model) and
statsmodels.tsa.SARIMAX. These will be removed after the 0.12 release.

statsmodels.tsa.arima.model.ARIMA makes use of the statespace framework and
is both well tested and maintained.

To silence this warning and continue using ARMA and ARIMA until they are
removed, use:

import warnings
warnings.filterwarnings('ignore', 'statsmodels.tsa.arima_model.ARMA',
                        FutureWarning)
warnings.filterwarnings('ignore', 'statsmodels.tsa.arima_model.ARIMA',
                        FutureWarning)

  warnings.warn(ARIMA_DEPRECATION_WARN, FutureWarning)

In [27]:

model_fit.summary()

Out[27]:

ARIMA Model Results

Dep. Variable:	D.Sales	No. Observations:	104
Model:	ARIMA(1, 1, 1)	Log Likelihood	-951.126
Method:	css-mle	S.D. of innovations	2227.263
Date:	Fri, 30 Apr 2021	AIC	1910.251
Time:	10:19:32	BIC	1920.829
Sample:	02-01-1964	HQIC	1914.536
	- 09-01-1972

	coef	std err	z	P>|z|	[0.025	0.975]
const	22.7843	12.405	1.837	0.066	-1.530	47.098
ar.L1.D.Sales	0.4343	0.089	4.866	0.000	0.259	0.609
ma.L1.D.Sales	-1.0000	0.026	-38.503	0.000	-1.051	-0.949

Roots

	Real	Imaginary	Modulus	Frequency
AR.1	2.3023	+0.0000j	2.3023	0.0000
MA.1	1.0000	+0.0000j	1.0000	0.0000

In [28]:

df['forecast']=model_fit.predict(start=90,end=103,dynamic=True)
df[['Sales','forecast']].plot(figsize=(12,8))

Out[28]:

<AxesSubplot:xlabel='Month'>

SARIMA MODEL

In [29]:

import statsmodels.api as sm

In [30]:

model=sm.tsa.statespace.SARIMAX(df['Sales'],order=(1, 1, 1),seasonal_order=(1,1,1,12))
results=model.fit()

/opt/conda/lib/python3.7/site-packages/statsmodels/tsa/base/tsa_model.py:527: ValueWarning: No frequency information was provided, so inferred frequency MS will be used.
  % freq, ValueWarning)
/opt/conda/lib/python3.7/site-packages/statsmodels/tsa/base/tsa_model.py:527: ValueWarning: No frequency information was provided, so inferred frequency MS will be used.
  % freq, ValueWarning)

In [31]:

df['forecast']=results.predict(start=90,end=103,dynamic=True)
df[['Sales','forecast']].plot(figsize=(12,8))

Out[31]:

<AxesSubplot:xlabel='Month'>

HERE THE BLUE LINE IS ACTUAL DATA & ORANGE LINE IS PREDICTED DATA. HOW GOOD IT GAVE US THE RESULTS.

---

4. PREDICT FOR FUTURE DATASET:

In [32]:

from pandas.tseries.offsets import DateOffset

#Here USING FOR LOOP we are adding some additional data for prediction purpose:

future_dates=[df.index[-1]+ DateOffset(months=x)for x in range(0,24)]

In [33]:

#Convert that list into DATAFRAME:

future_datest_df=pd.DataFrame(index=future_dates[1:],columns=df.columns)

In [34]:

future_datest_df.tail()

Out[34]:

	Sales	Seasonal First Difference	forecast
1974-04-01	NaN	NaN	NaN
1974-05-01	NaN	NaN	NaN
1974-06-01	NaN	NaN	NaN
1974-07-01	NaN	NaN	NaN
1974-08-01	NaN	NaN	NaN

In [35]:

#CONCATE THE ORIGINAL AND THE NEWLY CREATED DATASET FOR VISUALIZATION PURPOSE:
future_df=pd.concat([df,future_datest_df])

In [36]:

#PREDICT
future_df['forecast'] = results.predict(start = 104, end = 120, dynamic= True)  
future_df[['Sales', 'forecast']].plot(figsize=(12, 8))

Out[36]:

<AxesSubplot:>

Hence, We have predicted the SALES for the next Two Years Successfully.

---

In this Kernel I have shared basics to implementaion part of TIME SERIES | ARIMA MODEL | SARIMAZ MODEL using the added dataset.